Quite often in structural engineering we make simplifications to make things easier for ourselves. Sometimes they are conservative, sometimes not. Sometimes we are happy living in denial regarding the differences that might exist form doing something in a more ‘correct’ manner, sometimes not. It’s a matter of judgement.
One thing we often do is to simplify a series of regularly spaced point loads into an equivalent UDL. Do we ever worry ourselves on how accurate this really is? Today I got bored and decided to see at what point a UDL starts to accurately model series of point loads, just to give me something else to worry about in the future!
Common situations where we might do this is a simply supported primary beam supporting a series of secondary beams at a regular spacing (for my imperially challenged friends, you lot refer to girders which are primary beams and beams/joists which are secondary beams, same meaning basically). Instead of applying point loads to the primary beam we might estimate the actions based on an equivalent UDL.
Another scenario where you might be tempted to cheat could be a series of equally spaced fixings between a precast cladding panel and whatever steel member is supporting the panel (where loads can only transfer under face loading at the fixing locations).
I intend to answer the age-old question no one probably cared about, whether this equivalent UDL approach really satisfies being within some acceptable margin of error of the actual true answer compared with point loads.
Doing it…
So, what we are doing is if we had say a number of evenly spaced point loads of the same magnitude, we equate these loads to a UDL based on the beam spacing and point load. We then apply both load cases to a member and determine at which point we hit some acceptable margin in terms of differences.
For example, the moment/shear and deflection for 1, 2 and 3, etc point loads are shown below so you can see what’s going on. Point load results in BLUE, equivalent UDL in RED.

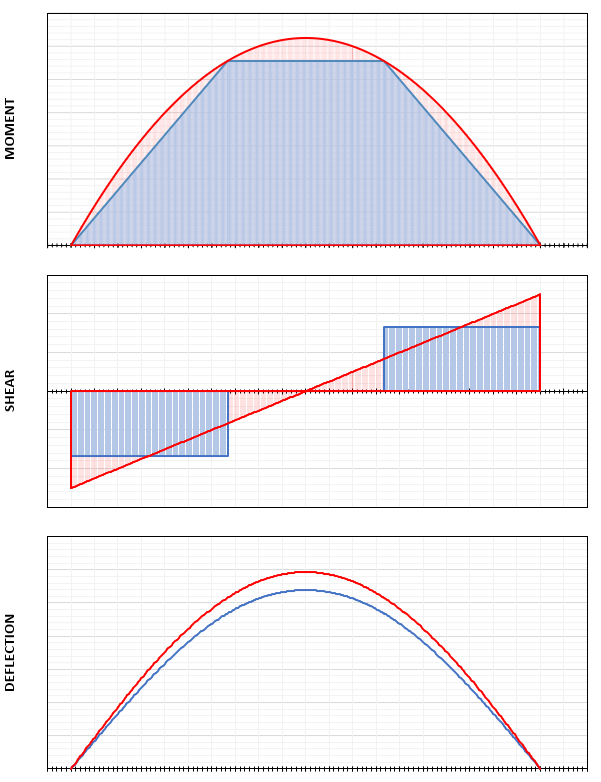

From the above hopefully you’ll notice in general with the UDL approach the following trends developing: –
- For moment, the equivalent UDL approach either equals or exceeds the point load maximum midspan moment. The moments at point load locations, always lies on the UDL envelope
- For an odd number of point loads the maximum moments are always equal
- For an even number of point loads the maximum moments from the equivalent UDL approach are conservative (always overestimated)
- For shear, the equivalent UDL approach is a train wreck. You’re underestimating or overestimating the shear depending on where you might be interested in evaluating the shear.
- In terms of the maximum shear, you are always going to overestimate this, the degree of overestimation really depends on the number of point loads you’re attempting to replace.
- For deflection, the equivalent UDL approach is always going to overestimate the deflection. Not as bad as the shear train wreck, but something to be mindful of when you’re cheating the system like this that the result is conservative
Now what’s an acceptable margin in terms of the closeness of the results before you even need to think about this kind of thing, 10%, 5%, 2.5%? I don’t know, so I broke out a few VBA loops to record the results of comparing max midspan moment, end span shear, and the midspan deflection from one point load to fifty point loads!
Accuracy…
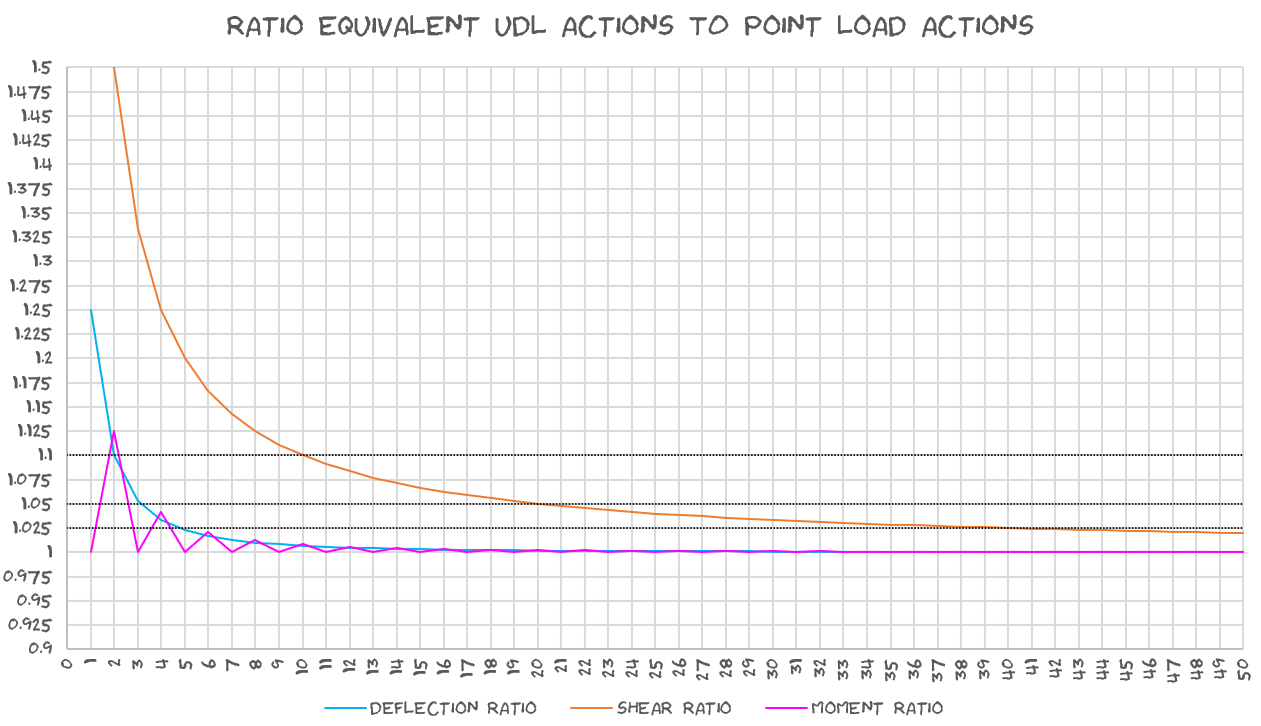
You can see for this plot that even for relatively few point loads, you’re potentially overestimating the maximum shear by up to 50%, that Trainwreck. Often in the case of steel beam design at least, shear isn’t usually much of a concern, so don’t sweat it.
For the moment, the maximum you’ll be out is about 12.5% if you were replacing two point loads with a UDL. By the time you get to 6 you’re less than 2.5% difference.
For the deflection, with two point loads being replaced, you’ll be within 10%. At five point loads being replaced with a UDL you’re within 2.5% of the true result. Probably good enough, I wouldn’t be losing any sleep over the moment or deflection is the moral of the storey.
If you’re the worrying type, concentrate on the shear.
If you’re replacing thirty nine point loads with an equivalent UDL, you can sleep safely in the knowledge that you’re within 2.5% of the true answer for your shear. 100% practical result!
Conclusions
What have we learned from this exercise: –
- If you have an uneven number of point loads, you’re picking up the max moment correctly.
- If you have an even number of point loads, you are not.
- Maximum deflection and maximum moment are always conservative when replacing with and equivalent UDL.
- Boredom and too much time on your hands makes you do some pointless stupid things sometimes.
In the case of an uneven number of point loads, how accurate your maximum moment is really depending on the number of point loads you’re trying to assess an equivalent UDL for? Suffice to say, you’ll always be conservative as the UDL equivalent moment is always higher than the peak moment from the series of point loads.
As far as shear goes, it’s a disaster. Don’t rely on the max shear being correct with any degree of confidence. Depending on the number of point loads and where you are interested in evaluating the shear along a members, you’ll be all over the show. If knowing the shear with a higher degree of accuracy is important to you. Then work it out correctly … no shortcuts.
Have I missed something in your rationale? If a beam supports a concentrated load W at midspan the moment is WL/4. If the same load is spread over the length of the beam the moment is WL/8 so assuming a UDL underestimates the moment by 50%.
Hi Bruce, thanks for the comment.
I think the logic I was trying to demonstrate was not one of spreading the point load over the entire beam, but more about taking in the case of one point load as load over half the beam (a tributary length if you like).
As that is the logic once you get into considering more point loads for an equivalent UDL load, if you have n=3 evenly spaced point loads at 1/4L, 1/2L and 3/4L , the tributary width for each point load is effectively 1/4 of the span for working out the equivalent UDL that one might design the entire beam length for to get an equivalent moment/shear for simplicity. The main point I was trying to make is this isn’t always equivalent obviously.
i.e. W/(L/(n+1)) equivalent UDL, so for a single central point load, the equivalent UDL would be UDL=W/(L/(1+1)), or based on 1/2 the length if that makes sense? So a UDL of 2W/L, so the UDL moment is 2W/L*L^2/8 = WL/4 QED, same as single central point load! Hope that makes sense 🙂
But yeah, I agree with what you are saying if you spread a single point load over the entire beam. Totally inaccurate!
So hopefully engineers are not doing this and are instead just working out the loading from a single point load, after all can’t get much simpler than this.
Thanks for clarifying. I like your blog by the way, great work!