Well after saying here that there was limited practical use for point moments for a simply supported beam, so I wasn’t going to (didn’t see a need to) include them. I’ve eaten those words now and added the ability to consider point moments.
Thanks to some work I’ve been doing recently at work on steel design using the alternative design provisions within NZS3404 for combined actions checks, I found a practical use for having applied moments considered in working out some of the parameters used. Yum words.
More on this use case in a later post I guess, but the deflection within a design segment subject to transverse loads is required to evaluate the βM factor using CL8.4.2.2.2 of NZS3404, which directs you to make βM = βT from CL4.4.3.2.4 if transverse loads are present, and this requires you to consider the deflection with end moments applied. All very convoluted!

Well to do this properly you obviously need to have the moments at the end of the segment applied like noted above…. Like I said earlier… Yum words…
A formulation for adding point moments anywhere on the main span and cantilever have been added to the beam formulae code module. Download the latest version here on GitHub.
The inputs for the moments follow the exact same logic as for the point loads, entered in a n rows by 2 column range or array for both the main span and the cantilever span, see part 2 for further info on this.
I’ve updated the BEAM_analysis function to have two further inputs (in bold): –
=BEAM_analysis(length_step, L_main, L_cant, E_beam, I_beam, Main_UDL, Main_PT, Main_PTM, Cant_UDL, Cant_PT, Cant_PTM, close_diagram, moment_shear_only)| length_step | The max distance step along the beam to derive the points at which results are to be returned |
| L_main | Main span beam length |
| L_cant | Cantilever span length |
| E_beam | Youngs modulus for the beam |
| I_beam | Moment of inertia of the beam |
| Main_UDL | Cell Range with UDL data for the main span |
| Main_PT | Cell Range with point load data for the main span |
| Main_PTM | Cell Range with point moment data for the main span |
| Cant_UDL | Cell Range with UDL data for the cantilever |
| Cant_PT | Cell Range with point load data for the cantilever |
| Cant_PTM | Cell Range with point moment data for the cantilever |
| close_diagram | Optional Boolean value to add extra data points to close off moment and shear diagrams to allow for plotting. |
| moment_shear_only | Optional Boolean value to select only returning Moment and Shear |
Examples with moments

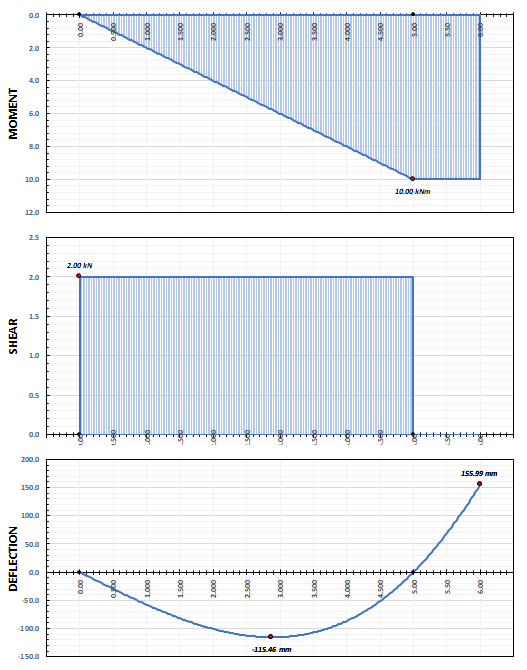
So now you can literally consider any type of loading possible, constant UDL’s, triangular UDL’s, trapezoidal UDL’s, point loads, point moments!
Fixed a small error for cantilever formulation..
I also noticed when doing earlier verification that while the answers for the cantilevers were always slightly different than the computer model used to verify the answers, they were still awfully close. Like noticing the second decimal place was out by some small margin. I put this down to some numerical precision creeping in and thought nothing more of it. But I have now discovered the error of my ways!
The issue was I was working using very small loads in the verification cases, so the deflections were very small. So while they appeared correct to several decimal places, they were in fact out by this very very small margin and it was impossible to notice any deviations between the correct answer and results obtained from the code.
Now scale this up to looking at a larger deflection case and the differences became more obvious in a recent practical case where I was using the spreadsheet. Looking into the code the culprit was I had enclosed some of the rotations in a TAN() function. No idea what I was thinking at the time in doing this, but the end result is this was incorrect and has now been corrected!
So, if you downloaded the previous version, make sure you update your code from the repository, or manually make the same correction noted in this commit.
Hello,
I am very interested to learn and see from your code there, very creative and fast with array method.
However, from the first look, i figured out that for some reason it cant run in Finnish format. I guess maybe from some List separator from “comma” and “semi-colon”, but as far as I know the syntax of the formula in both Excel and VBA should update automatically to the system. I am very curious what is the error which prevent it from working.
Looking forward to hearing from you soon
KR
Anh
Unfortunately I don’t know the answer here as only ever dealt with english!
What is the exact error you’re getting, perhaps you’re missing a reference or something in the VBA editor?
Hello, I’ve taken a look at the code. Really nice!
I am in Denmark, and I found out that the function determining the number of decimal places as a function of tolerance, needs to be updated. It is looking for a “.” instead of a “,” in the string search.
Thanks, I’ll try update this to be more generic!
This Excel file looks amazing to help with repeated beam calculations. Unfortunately, I’m having issues with it. When I open the file, I can see the data from the example, but as soon as I try to change a value I get an error saying Excel found a problem with one or more formula references in this worksheet.
On the right in the grey section, the first row under X shows #VALUE! and the moment and shear are empty. The calculated MAX values below all show #REF!
I understand this post dates back to a few years, but if you know how to fix this issue it would be awesome!
Thanks!