Well, one person’s world of torsion anyway…
In this post I’ll show how to use Mathematica to check some derivatives of torsion relationships.
Mathematica is an analysis/computational tool by Wolfram. Now if you had to pony up the dollars for it you’d be out a few thousand dollars, but as it happens I’m cheap and it’s free on Raspberry Pi’s Raspbian operating system. Yes it’s linux based, but don’t let that turn you off, it’s so simple to setup anyone could do it.
I have zero idea if the Raspberry Pi version is feature limited in any way, in comparison to getting fleeced for some serious coin. But free is free, and so far I’ve not had any issues solving anything I throw at it.
The downside of running on such low power hardware is that it can take time to solve anything mildly complex, but you live with it for the price.
Why are we doing this, we’ll in this EngTips post the poster seemed to show some disagreement with the published solutions which were kindly provided by AISC in the paper titled ‘Technical Note: Torsional Analysis of Steel Sections, 2002 Engineering Journal, fourth quarter‘. A search of the internet should easily yield you a copy, or download a version from the linked thread.
So let’s set about seeing if we agree or not with the AISC answers by undertaking the necessary derivatives in Mathematica.
Let’s pick on case 11, as it was identified as having an incorrect sign in one of the terms. So i’ll take my own advice and “just” do the derivatives. Easy right….
With Mathematica to the rescue (read it’s been a while since I had to use calculus in anger and cannot remember how or words to that effect)…. Easy right (now) …
If I had to compare Mathematica to something I’d say it’s sort of Mathcad like in the way you enter problems. There also seems to be a wealth of information on the Internet related to running analyses which is pretty helpful to get a handle on the exact nomenclature to use. It’s a bit finicky about this, one thing out of place and you’ll be graced with a non descript error or nothing occurring when you evaluate your expressions. With little or no idea what you did wrong. Similarly for some reason the nomenclature Mathematica uses differs slightly from the online Wolframalpha site which is based on the same analysis engine (both must have been designed by engineers right).
One other thing, while Wolframalpha might be able to be used, you’ll reach a limit on what it can do before it asks you for dollars as you may hit an arbitrary computation limit depending on how complex the expressions are that you are trying to evaluate. But the free on Raspberry Pi version doesn’t seem to have any such limitations (as far as I’m aware).
So anyway, for case 11, the angle is given as:-
![Rendered by QuickLaTeX.com \theta=\displaystyle{\frac{ta^2} {GJ}\Bigg[ \bigg[1-\frac{5L^2}{6a^2}-\bigg(\frac{a}{L}-\frac{L}{2a}\bigg) \text{Tanh}\frac{L}{a} \bigg]+ \bigg[-\frac{z}{L}+\frac{zL}{a^2}\bigg]+ \bigg[\frac{a}{L}-\frac{L}{2a} \bigg]\Bigg(\frac{ \text{Sinh}\displaystyle{\frac{z}{a}}}{ \text{Cosh}\displaystyle{\frac{L}{a}}}\Bigg)-\frac{z^2}{6a^2}\frac{z}{L} \Bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-43d1ea38c61c2e84a44c37bf5df7b7f4_l3.png)
where ![]()
Well bugger me if I had to differentiate that obscenity by hand to find ![]() or
or ![]() or even
or even ![]() , I’m the first to admit I don’t even know where to start simply because it looks intimidating. Oh my cosh hyperbolic functions scare me alright, it’s pretty hard to take a sinh to them… bad, but had to be done.
, I’m the first to admit I don’t even know where to start simply because it looks intimidating. Oh my cosh hyperbolic functions scare me alright, it’s pretty hard to take a sinh to them… bad, but had to be done.
AISC formulas for the derivatives are given below:-
![Rendered by QuickLaTeX.com \theta '=\displaystyle{\frac{ta} {GJ}\Bigg[-\frac{a}{L}+\frac{L}{a}+\bigg(\frac{a}{L}-\frac{L}{2a}\bigg)\Bigg( \frac{\text{ Cosh}\displaystyle{\frac{z}{a}}}{\text{Cosh}\displaystyle{\frac{L}{a}}} \Bigg)-\frac{z^2}{2aL} \Bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-3fec9746764f170773ebbcecb3260e28_l3.png)
![Rendered by QuickLaTeX.com \theta ''=\displaystyle{\frac{t} {GJ}\Bigg[\bigg(\frac{a}{L}+\frac{L}{2a}\bigg)\Bigg( \frac{\text{Sinh}\displaystyle{\frac{z}{a}}}{ \text{ Cosh}\displaystyle{\frac{L}{a}}} \Bigg)-\frac{z}{L} \Bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-80990514f992781d0c6af10975e1f119_l3.png)
![Rendered by QuickLaTeX.com \theta '''=\displaystyle{\frac{t} {GJa}\Bigg[\bigg(\frac{a}{L}-\frac{L}{2a}\bigg)\Bigg( \frac{ \text{Cosh}\displaystyle{\frac{z}{a}}}{ \text{ Cosh}\displaystyle{\frac{L}{a}}} \Bigg)-\frac{a}{L} \Bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-70807b521b6818b772919cd785563886_l3.png)
So lets see if Mathematica gives us the same answers, this is the code you’d enter for taking the first/second & third derivative of the function. The ![]() simply means you are using the previous answer ‘
simply means you are using the previous answer ‘![]() ‘ as an input and differentiating this with respect to
‘ as an input and differentiating this with respect to ![]() , similarly
, similarly ![]() would mean using the answer from two answers previous.
would mean using the answer from two answers previous.
Just enter these into Mathematica, one after the other and select Evaluation>Evaluate Notebook from the menus to solve.

Then a few seconds later we’ll get the following answers, original function, first, second and third derivatives:-
While they take a slightly different form, I can assure you with some simplification they give the same answer as the AISC output apart from the second derivative which does indeed seem to contain an incorrect sign. For example:-
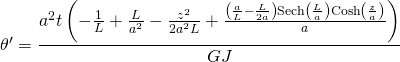
By factoring out and simplifying the ![]() variables, and recognising that
variables, and recognising that ![]() , and throw in some rearranging of the location of the terms then this answer simplifies to the following expression:-
, and throw in some rearranging of the location of the terms then this answer simplifies to the following expression:-
![Rendered by QuickLaTeX.com \theta '=\displaystyle{\frac{ta} {GJ}\Bigg[-\frac{a}{L}+\frac{L}{a}+\bigg(\frac{a}{L}-\frac{L}{2a}\bigg)\Bigg( \frac{ \text{ Cosh}\displaystyle{\frac{z}{a}}}{ \text{Cosh}\displaystyle{\frac{L}{a}}} \Bigg)-\frac{z^2}{2aL} \Bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-29b6069e8cca66c0815d12454e88a8e8_l3.png)
Which is the same as the AISC answer….QED.
Similarly for the second derivative we can take the Mathematica answer given below and simplify it to the second expression in a similar manner:-
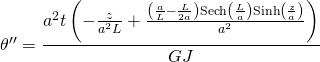
![Rendered by QuickLaTeX.com \theta ''=\displaystyle{\frac{t} {GJ}\Bigg[\bigg(\frac{a}{L}-\frac{L}{2a}\bigg)\Bigg( \frac{ \text{Sinh}\displaystyle{\frac{z}{a}}}{ \text{Cosh}\displaystyle{\frac{L}{a}}} \Bigg)-\frac{z}{L} \Bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-b4470eca6d06a8d0b37eccfe170cc7ac_l3.png)
Which as you’ll note has a ![]() term while the AISC answer has a
term while the AISC answer has a ![]() . No QED!, no cigar!…
. No QED!, no cigar!…
Finally the third derivative can be simplified in a similar manner by rearranging the ![]() terms and replacing the
terms and replacing the ![]() term:-
term:-
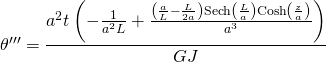
![Rendered by QuickLaTeX.com \theta '''=\displaystyle{\frac{t} {GJa}\Bigg[\bigg(\frac{a}{L}-\frac{L}{2a}\bigg)\Bigg( \frac{ \text{Cosh}\displaystyle{\frac{z}{a}}}{ \text{ Cosh}\displaystyle{\frac{L}{a}}} \Bigg)-\frac{a}{L} \Bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-70807b521b6818b772919cd785563886_l3.png)
Conclusion
World saved. Job done.
Seems like there is actually an error in the AISC formula, don’t believe everything you find on the internet I guess.
But more importantly we’ve shown how simple it is to use Mathematica to evaluate derivatives. It’s far more powerful than this of course.
So grab yourself a Raspberry Pi to check it out for a few dollars, or alternatively spend a few thousand dollars for a desktop version.
[EDIT] …Wait a minute….
Well this is embarrassing, it seems in September 2019 AISC updated their errata for Design Guide 9. It includes the following correction to Case 11 (and a few others being questioned in the original EngTips post):-
![Rendered by QuickLaTeX.com \theta=\displaystyle{\frac{ta^2} {GJ}\Bigg[ 1+\frac{L^2}{6a^2}-\bigg(\frac{a}{L}+\frac{L}{2a}\bigg) \text{Tanh}\frac{L}{a}-\frac{z}{L}+ \bigg[\frac{a}{L}+\frac{L}{2a} \bigg]\Bigg(\frac{ \text{Sinh}\displaystyle{\frac{z}{a}}}{ \text{Cosh}\displaystyle{\frac{L}{a}}}\Bigg)-\frac{z^3}{6La^2} \Bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-b0b14cf47547a0a673210ce325cdea12_l3.png)
So like I said don’t believe everything you find on the internet, inclusive of the original post above!
This correction of course impacts on all the derivatives, which are given below for completeness:-

These simplfy down to the following expressions in a similar form to that originally given by AISC:-
![Rendered by QuickLaTeX.com \theta '=\displaystyle{\frac{ta} {GJ}\Bigg[-\frac{a}{L}+\bigg(\frac{a}{L}+\frac{L}{2a}\bigg)\Bigg( \frac{ \text{ Cosh}\displaystyle{\frac{z}{a}}}{ \text{Cosh}\displaystyle{\frac{L}{a}}} \Bigg)-\frac{z^2}{2aL} \Bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-ba9c2e435e3483e761296ae24daa6260_l3.png)
![Rendered by QuickLaTeX.com \theta ''=\displaystyle{\frac{t} {GJ}\Bigg[\bigg(\frac{a}{L}+\frac{L}{2a}\bigg)\Bigg( \frac{ \text{Sinh}\displaystyle{\frac{z}{a}}}{ \text{Cosh}\displaystyle{\frac{L}{a}}} \Bigg)-\frac{z}{L} \Bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-02295cb8a95b49d0b3ea0a0fbf3831e8_l3.png)
![Rendered by QuickLaTeX.com \theta '''=\displaystyle{\frac{t} {GJa}\Bigg[\bigg(\frac{a}{L}+\frac{L}{2a}\bigg)\Bigg( \frac{ \text{Cosh}\displaystyle{\frac{z}{a}}}{ \text{ Cosh}\displaystyle{\frac{L}{a}}} \Bigg)-\frac{a}{L} \Bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-f0ed0cef6909efd8aaa11d3a2c83cdd3_l3.png)
Conclusion #2
So in conclusion (again), if you think you’ve found an error in something check in the first instance for an errata by the publisher. Then run screaming for the internet and Google.