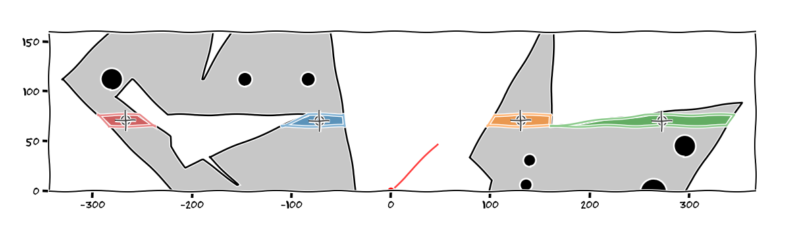
Part 5 – Centroids, More Integrals….
In the last post we went through a process to find a general force integral which involved knowing the width and height of the stress block in terms of how far from the neutral axis depth you are. Then by using numerical integration methods we would be able to calculate the concrete force by evaluating this integral. Note that except for certain cases like a constant stress or constant width I don’t think you can even solve the integral by hand, so your best chance of success is solving it numerically unless of course you’re a masochist and love integration that much. Good thing Python makes it easy to solve integrals numerically.
In this post we’ll look at extending the previous post (and the result we had magicked up for the force integral) by going on to find the centroid, or in other words the location where the resultant force acts within our concrete compression block.
I must admit that at first this aspect of the calculations confused the hell out of me. Most examples I could find say stuff like the following integral is the general integral to use to find the centroid of a general 3D volume. So easy just work this out and we are done:-
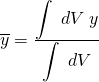
Well its all good saying that, but without any solid examples to follow I was at a loss as to what exactly I needed to do at this point. It was confusing in the sense that what the hell was I supposed to be integrating, what is ![]() in the context of our particular problem? I drew a blank until I found a few examples with enough detail to throw me in the right direction.
in the context of our particular problem? I drew a blank until I found a few examples with enough detail to throw me in the right direction.
So I’ll try break it down in relatively simple terms as to what my thought process eventually was, and how it all (eventually) made sense to me (at least).
Show me the centroid!…
For a moment lets consider the fact that every engineer is probably taught how to find the centroid of a simple composite 2D area made up of other constituent shapes which they know the centroid of like triangles, rectangles, etc. In a easy form to relate to, we can simply say the following for ![]() individual elements:-
individual elements:-
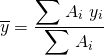
Looks familiar I bet… easy right? We all passed 1st year engineering I hope and came across this concept before. So it stands to reason that we could also write the following expression for finding the centroid of a volume working along the same lines as using areas:-
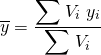
Examining the terms in this equation, we could say in pseudo-code that the centroid equation is simply the sum of a whole lot of volumes multiplied by the distance to the centroid of these volumes (a lever-arm from some datum if you like) divided by the sum of all the volumes being considered.
Extending this concept a little, another way to consider the above relationship is as an integral for a general volume. That is the sum of a whole lot of little infinitely small volumes multiplied by the distances to the centroid of the little volumes (from some datum) divided by the total sum of all the little volumes. The difference is we are talking about dividing things up into infinitesimally small sized volumes, but otherwise its all exactly the same concept. This would be similar to writing in integral form the following:-
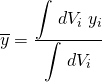
or simply removing the subscript for clarity:-
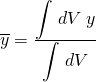
The keen eyed among you will note that this is essentially the same as the first integral noted above that caused my initial confusion, cool, it’s starting to make sense hopefully. Now it’s dawning on me that ![]() is simply some expression for a small bit of volume (or force in our problem).
is simply some expression for a small bit of volume (or force in our problem).
Given that we spent the last post determining the force from summing up (integrating) a whole lot of small bits of force to find the total force, and the force was sort of treated in the derivation as being equivalent to the volume we were trying to find. Then couldn’t we simply substitute in the previous equation for a little bit of force/volume into our centroid equation, substituting our little bit of force ![]() being equal to the little bit of volume
being equal to the little bit of volume ![]() .
.
So substituting the following (assuming a section/compression block with linearly varying sides and being in the parabolic part of the Eurocode 2 curve):-
![]() … remember this …
… remember this …
![]()
into the general equation above for ![]() gives the following integral:-
gives the following integral:-
![Rendered by QuickLaTeX.com \overline{y}\;=\;\frac{\displaystyle{\int}\;dV\;y}{\displaystyle{\int}\;dV} \;=\;\frac{\displaystyle{\int}\;\bigg[\displaystyle{\frac{(x_1-x_2)(y_2-y)}{(y_2-y_1)}}+x_2\bigg]\;\bigg[(1-(1-\displaystyle{\frac{y}{k_1c}})^n\bigg]\; \bigg[y\bigg]\;\bigg[dy\bigg]}{\displaystyle{\int}\;\bigg[\displaystyle{\frac{(x_1-x_2)(y_2-y)}{(y_2-y_1)}}+x_2\bigg]\;\bigg[(1-(1-\frac{y}{k_1c})^n\bigg]\;\bigg[dy\bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-c6f3b9ef7a45a9bb1f57d4efbfedb1b8_l3.png)
Low and behold, we now have a general equation for the ![]() direction centroid for the parabolic region of the stress block with linearly varying sides. I believe in the beginning I suggested in the first post in this series that this was going to be simple, and well that was kind of simple if you break it down and compar to stuff you already know how to calculate that has similarities (come on who believed me…).
direction centroid for the parabolic region of the stress block with linearly varying sides. I believe in the beginning I suggested in the first post in this series that this was going to be simple, and well that was kind of simple if you break it down and compar to stuff you already know how to calculate that has similarities (come on who believed me…).
Similar to the force integral, the integrals can therefore be written in terms of evaluating the centroid between two limits ![]() &
& ![]() . We know all of the variables, as they are all the same as the force derivation. Everything is also written in terms of
. We know all of the variables, as they are all the same as the force derivation. Everything is also written in terms of ![]() which we are integrating with respect to (the
which we are integrating with respect to (the ![]() bit), so we arrive at the following expression:-
bit), so we arrive at the following expression:-
![Rendered by QuickLaTeX.com \overline{y}\;=\;\frac{\displaystyle{\int_{y_1}^{y_2} }\;\bigg[\displaystyle{\frac{(x_1-x_2)(y_2-y)}{(y_2-y_1)}}+x_2\bigg]\;\bigg[(1-(1-\displaystyle{\frac{y}{k_1c}})^n\bigg]\; \bigg[y\bigg]\; \bigg[dy\bigg]}{\displaystyle{\int_{y_1}^{y_2} }\;\bigg[\displaystyle{\frac{(x_1-x_2)(y_2-y)}{(y_2-y_1)}}+x_2\bigg]\;\bigg[(1-(1-\frac{y}{k_1c})^n\bigg]\;\bigg[dy\bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-5e03305a2ba32869b0d3fb0c7303f425_l3.png)
Note that the numerator is simply the force integral multiplied by an extra ![]() (a lever-arm if you like), and the denominator is just the previous force integral (so hopefully we can get away with only evaluating it once, though as it turns out solving the integrals is pretty fast in python). So basically we satisfy our pseudo-code explanation for finding a centroid, or resultant force location, i.e. a sum of forces multiplied by lever-arms, divided by a sum of forces.
(a lever-arm if you like), and the denominator is just the previous force integral (so hopefully we can get away with only evaluating it once, though as it turns out solving the integrals is pretty fast in python). So basically we satisfy our pseudo-code explanation for finding a centroid, or resultant force location, i.e. a sum of forces multiplied by lever-arms, divided by a sum of forces.
We can also derive other relationships for shapes with sides that vary in other ways, or for other stress/strain relationships as noted in the force derivation. All we need to be mindful of is that these expressions for the ![]() and
and ![]() terms simply need to be written in terms of
terms simply need to be written in terms of ![]() since we are integrating with respect to
since we are integrating with respect to ![]() , then we are golden.
, then we are golden.
It follows as you would expect that for the ![]() direction centroid that it works in a similar way. The little bits of force are the same for our thin slices of volume, but the lever-arm is now an
direction centroid that it works in a similar way. The little bits of force are the same for our thin slices of volume, but the lever-arm is now an ![]() distance from some datum. Given we already worked out the relationship for the
distance from some datum. Given we already worked out the relationship for the ![]() of the region in compression at any
of the region in compression at any ![]() value when working through the force derivation, the
value when working through the force derivation, the ![]() direction lever-arm is simply the distance to the center of this width of our infinitely thin slice of force/volume.
direction lever-arm is simply the distance to the center of this width of our infinitely thin slice of force/volume.
Now since we already know the location of the edges of our compression area (from the fundamental geometry in our defined section) and if the sides vary linearly, then if you connect the midpoint of the top and bottom widths of the compression area with an imaginary vertical line then the centroid of each little horizontal slice of force lies on this line. So all we need is an equation for this imaginary line written in terms of ![]() and we then have an relationship for the
and we then have an relationship for the ![]() lever-arm for a given
lever-arm for a given ![]() .
.
This relationship can be derived in the following form, noting that we have defined values for the ![]() coordinates of the midpoint of the top and bottom widths of our compression area to simplify things:-
coordinates of the midpoint of the top and bottom widths of our compression area to simplify things:-
![]()
Now that we have this, it’s simply a matter of swapping out the lever-arm value. In the ![]() direction centroid equation this was simply the
direction centroid equation this was simply the ![]() that’s in the numerator. So substituting
that’s in the numerator. So substituting ![]() into an equivalent
into an equivalent ![]() direction centroid equation yields the following general integral for the
direction centroid equation yields the following general integral for the ![]() direction centroid:-
direction centroid:-
![Rendered by QuickLaTeX.com \overline{x}=\frac{\displaystyle{\int_{y_1}^{y_2}}\;\bigg[\frac{(x_1-x_2)(y_2-y)}{(y_2-y_1)}+x_2\bigg]\;\bigg[(1-(1-\displaystyle{\frac{y}{k_1c}})^n\bigg]\;\bigg[\frac{(x_{b\,mid}-x_{t\,mid})(y_2-y)}{(y_2-y_1)}+x_{t\,mid}\bigg]\;\bigg[dy\bigg]}{\displaystyle{\int_{y_1}^{y_2}}\;\bigg[\frac{(x_1-x_2)(y_2-y)}{(y_2-y_1)}+x_2\bigg]\;\bigg[(1-(1-\displaystyle{\frac{y}{k_1c}})^n\bigg]\;\bigg[dy\bigg]}](https://engineervsheep.com/wp-content/ql-cache/quicklatex.com-e8a3309f256423bc3763742836626c75_l3.png)
Conclusion
So having gone full circle in a way, we are back at where we started in part 1 having derived the first horrible looking integral that was listed. To go along with this we have derived a ‘simple’ set of equations for forces and centroids in each direction, exactly as advertised.
While I’ve worked with the EC2 parabolic part of the stress block here and sections with linearly varying sides, really any sort of stress block or section shape can be used. For example if you have a constant width, then the ![]() term turns into a constant, for a rectangular stress block the
term turns into a constant, for a rectangular stress block the ![]() term simply turns into a constant. Just simply swap out the various terms for
term simply turns into a constant. Just simply swap out the various terms for ![]() and
and ![]() to suit, and the same general approach applies.
to suit, and the same general approach applies.
Wasn’t to bad really was it… Forces and centroid theory lesson over, time to implement this in our Python code in the next post (more pictures next time I promise).